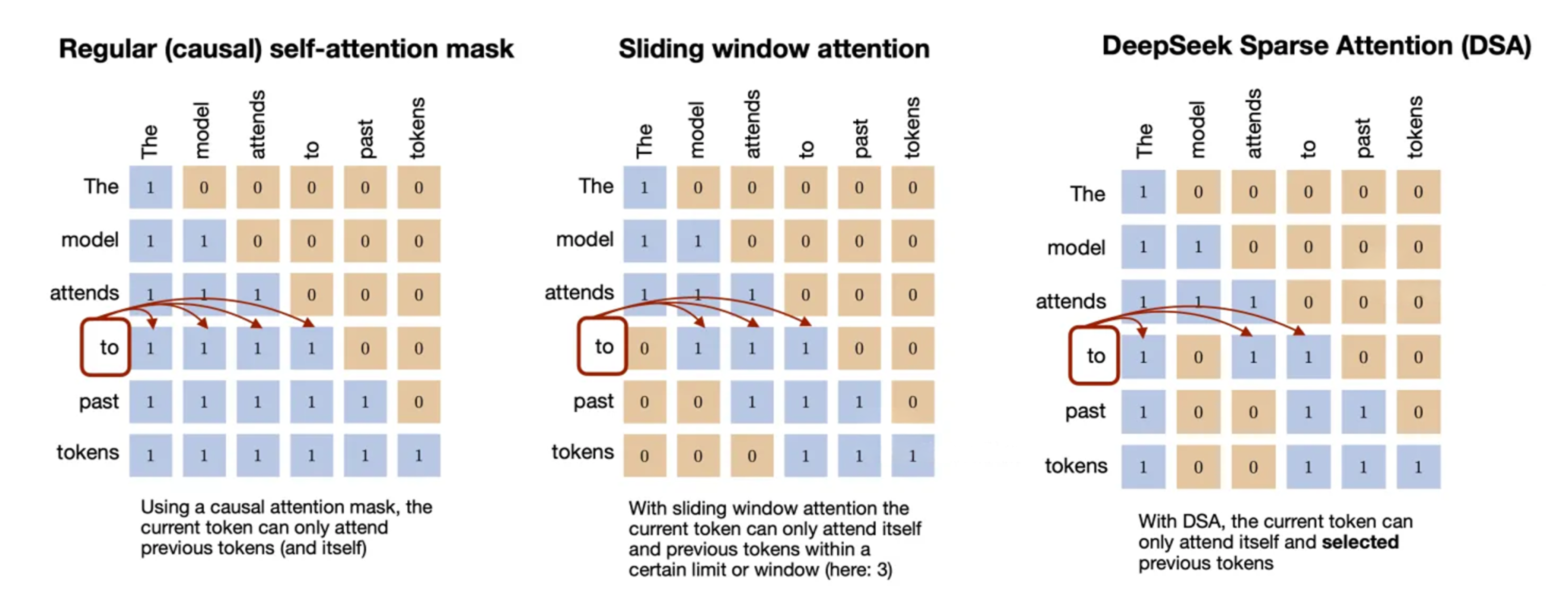
DeepSeek Sparse Attention (DSA)

likchern: 谁家好人休息是去研究 sparse attn 怎么实现的，特别还是在赶论文的时候 (￣ε(#￣)

简介

为了适应长上下文场景，DSA 通过只保留 top-k tokens 参与计算，将 attn 计算从 \(\mathcal{O}\left(L^2\right)\) 降低到 \(\mathcal{O}\left(L\cdot k\right)\)

DSA 的思想借鉴自 sliding window attention（当前 query token 只关注一个固定窗口的子集，位置相近度优先），通过 indexer 和 token selector 选择从过去的所有 token 中选择哪些可以被关注（语义相关性优先），使得选择更加随机

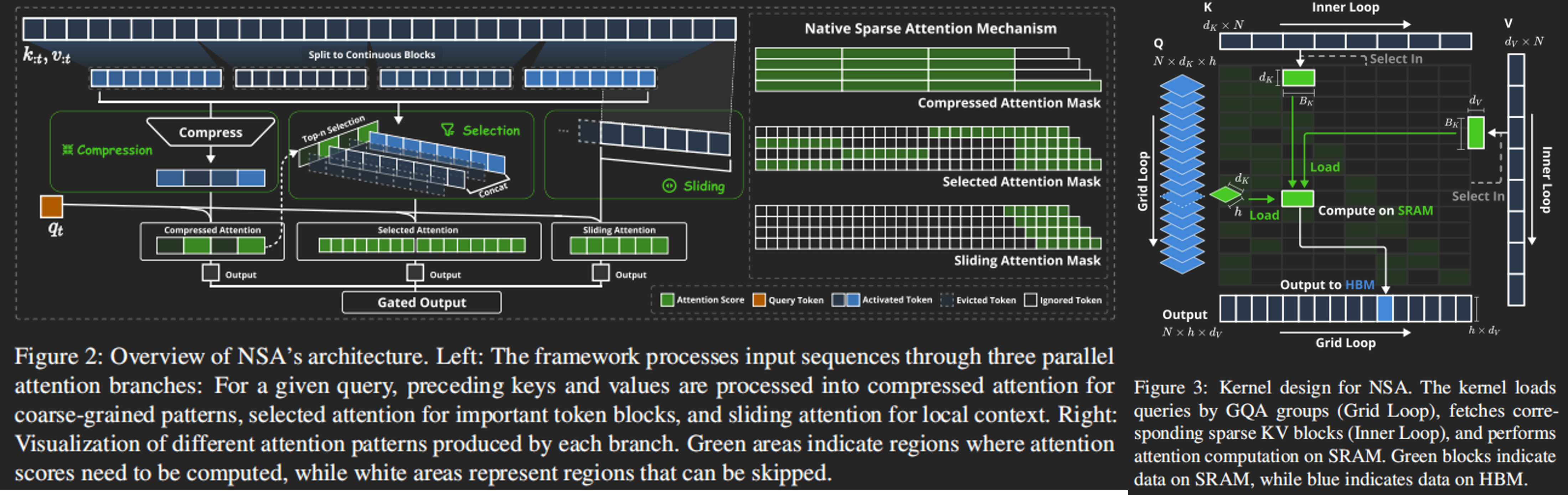
稍微了解后发现是在先前 ACL'25_Native-Sparse-Attn 的基础上将 Sliding 替换为 Indexing，加上原本的 Compression 和 Selection 整合进 Indexer 中

其中，Selection 的 kernel 实现从 Triton 改成 TileLang，策略不变：在沿用的 Sparse Attn 中，GQA 或 MQA 的每个 query head 共享 KV$， 将整个 group 直接加载到 smem 上，避免 naive attn 中跨 KV block query 的情况

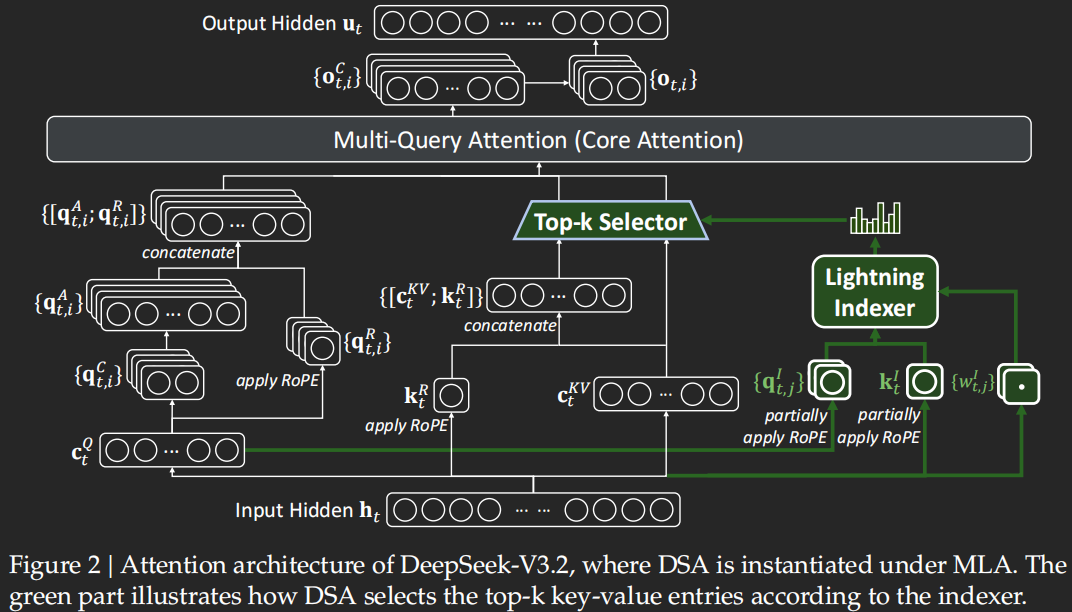
DSA 在原本 MLA 的基础上增加了 Lightning Indexer 和 Top-k Selector（图中 绿色 通路），基于所有先前的 token 为每个新的 query token 计算 index score

实现

原理

Lightning Indexer 的计算沿用 key-query 思想，原本的 attention score 即 index score，输入包括：

• 从 query token \(\mathbf{h}_{t}\) 映射得到的 query emb \(\mathbf{q}_{t,j}^I \in \mathbb{R}^{d^I}\) 与 weight \(w_{t,j}^I \in \mathbb{R}\)
• 从序列中先前的token \(\mathbf{h}_{s}\) 映射得到的 key emb \(\mathbf{k}_s^I \in \mathbb{R}^{d^I}\)

在 Indexer 中，通过 \(H^I\)-heads key-query 计算出 index score

\[ I_{t,s}=\sum_{j}^{H^I} w_{t,j}^I \cdot \text{ReLU}\left(\mathbf{q}_{t,j}^I \cdot \mathbf{k}_s^I \right) \]

注意到这里使用的是 ReLU 而非 Softmax，保证不会放大负噪声的同时使计算量对 FP8 更友好

计算完 index score 后，Top-k Selector 选出 \(\left\{I_{t,s}\right\}\) 中 top-k 对应的 KV-entry 参与最后的 Attention 计算

代码

核心代码 在 inference/model.py 中，主要观察 Indexer.forward()：

1. 将 query token qr 通过一层 Linear 映射到 query emb，然后做 partial RoPE

   q = self.wq_b(qr)
   q = q.view(bsz, seqlen, self.n_heads, self.head_dim)
   q_pe, q_nope = torch.split(
       q, [self.rope_head_dim, self.head_dim - self.rope_head_dim], dim=-1
   )
   # rope in indexer is not interleaved
   q_pe = apply_rotary_emb(q_pe, freqs_cis, False)
   q = torch.cat([q_pe, q_nope], dim=-1)
   

   DSA 的核心是语义相关性优先，即选出语义强相关的 token，如果使用全维 RoPE 会强行把所有位置信息编码进 query emb 中，使其变得位置敏感

   对此，DSA 将 query emb 拆分成 RoPE（局部顺序）和 Non-RoPE（全局语义）两个子空间，让 Indexer 自然偏向后者（后面要做 Hadamard Transform）

2. 从输入 x 经过 Linear + LayerNorm 得到 key emb，同样也是做 partial RoPE

   k = self.wk(x)
   k = self.k_norm(k)
   k_pe, k_nope = torch.split(
       k, [self.rope_head_dim, self.head_dim - self.rope_head_dim], dim=-1
   )
   # rope in indexer is not interleaved
   k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis, False).squeeze(2)
   k = torch.cat([k_pe, k_nope], dim=-1)
   

3. 对 query emb 和 key emb 进行 Hadamard Transform，使 q/k emb 的能量分布变得均匀

   Hadamard Transform

   def rotate_activation(x: torch.Tensor) -> torch.Tensor:
       assert x.dtype == torch.bfloat16
       from fast_hadamard_transform import hadamard_transform
   
       hidden_size = x.size(-1)
       return hadamard_transform(x, scale=hidden_size**-0.5)
   
   q = rotate_activation(q)
   k = rotate_activation(k)
   

   partial RoPE 导致 q/k emb 的能量分布不均匀，直接稀疏选择会被能量大的部分主导

   Hadamard Transform 作为一种完全确定且可逆的 正交变换（\(\mathcal{O}(n\log n)\)，bit-flip + add），把每个输出维度变成所有输入维度的均匀线性组合，从而使得能量分布变均匀，常用于 sparse routing 中

4. 到上一步都是 BF16，这一步 quant 到 FP8 减少计算

   q_fp8, q_scale = act_quant(q, block_size, self.scale_fmt)
   k_fp8, k_scale = act_quant(k, block_size, self.scale_fmt)
   

   act_quant caller 将 emb 规整成 "block 对齐、scale明确" 的 FP8 tensor

   def act_quant(
       x: torch.Tensor, block_size: int = 128, scale_fmt: Optional[str] = None
   ) -> Tuple[torch.Tensor, torch.Tensor]:
       """
       Quantizes the input tensor `x` using block-wise quantization.
   
       Args:
           x (torch.Tensor): The input tensor to be quantized. Must be contiguous and its last dimension size must be divisible by `block_size`.
           block_size (int, optional): The size of the blocks to be used for quantization. Default is 128.
           scale_fmt (Optional[str], optional): The format of the scale. Default is None.
       Returns:
           Tuple[torch.Tensor, torch.Tensor]: A tuple containing:
               - The quantized tensor with dtype `torch.float8_e4m3fn`.
               - A tensor of scaling factors with dtype `torch.float32`.
       """
       assert x.is_contiguous(), "Input tensor must be contiguous"
       assert (
           x.size(-1) % block_size == 0
       ), f"Last dimension size must be divisible by block_size (block_size={block_size})"
       N = x.size(-1)
       y = torch.empty_like(x, dtype=torch.float8_e4m3fn)
       s = x.new_empty(*x.size()[:-1], N // block_size, dtype=torch.float32)
       kernel = act_quant_kernel(N, round_scale=scale_fmt is not None)
       kernel(x.view(-1, N), y.view(-1, N), s.view(-1, N // block_size))
       return y, s
   

   而 act_quant_kernel 则是基于 TileLang 实现 FP8 act block-wise quant 算子

   @tilelang.jit(pass_configs=pass_configs)
   def act_quant_kernel(
       N, in_dtype=BF16, out_dtype=FP8, scale_dtype=FP32, round_scale=False
   ):
       M = T.symbolic("M")
       fp8_min = -448.0
       fp8_max = 448.0
       fp8_max_inv = 1 / fp8_max
       num_stages = 0 if round_scale else 2
       blk_m = 32
       group_size = 128
   
       @T.prim_func
       def act_quant_kernel_(
           X: T.Tensor[(M, N), in_dtype],
           Y: T.Tensor[(M, N), out_dtype],
           S: T.Tensor[(M, T.ceildiv(N, group_size)), scale_dtype],
       ):
           with T.Kernel(T.ceildiv(M, blk_m), T.ceildiv(N, group_size), threads=128) as (
               pid_m,
               pid_n,
           ):
               x_shared = T.alloc_shared((blk_m, group_size), in_dtype)
               x_local = T.alloc_fragment((blk_m, group_size), in_dtype)
               amax_local = T.alloc_fragment((blk_m,), scale_dtype)
               s_local = T.alloc_fragment((blk_m,), scale_dtype)
               y_local = T.alloc_fragment((blk_m, group_size), out_dtype)
               y_shared = T.alloc_shared((blk_m, group_size), out_dtype)
   
               for _ in T.Pipelined(1, num_stages=num_stages):
                   T.copy(X[pid_m * blk_m, pid_n * group_size], x_shared)
                   T.copy(x_shared, x_local)
                   T.reduce_absmax(x_local, amax_local, dim=1)
                   for i in T.Parallel(blk_m):
                       amax_local[i] = T.max(amax_local[i], 1e-4)
                       if round_scale:
                           s_local[i] = fast_round_scale(amax_local[i], fp8_max_inv)
                       else:
                           s_local[i] = amax_local[i] * fp8_max_inv
                   for i, j in T.Parallel(blk_m, group_size):
                       y_local[i, j] = T.clamp(
                           x_local[i, j] / s_local[i], fp8_min, fp8_max
                       )
                   for i in T.Parallel(blk_m):
                       S[pid_m * blk_m + i, pid_n] = s_local[i]
                   T.copy(y_local, y_shared)
                   T.copy(y_shared, Y[pid_m * blk_m, pid_n * group_size])
   
       return act_quant_kernel_
   

   对形状 (M, N) 的输入，沿 N维 按 group_size=128 为 block、沿 M维 按 blk_m=32 为 tile，于是对于每个 (32, 128) 的 tile：

   1. L33：计算每一行的 absmax
   2. L35-39：按照 FP8 e4m3 进行 scaling
   3. L41-43：将 quant 到的数值 clamp 到 FP8 范围中

5. 存入Indexer 内部维护的 K cache 中

   self.k_cache[:bsz, start_pos:end_pos] = k_fp8
   self.k_scale_cache[:bsz, start_pos:end_pos] = k_scale
   

6. 从输入 x 经过 Linear 后归一化得到 weight，配合 query emb 所以还要 scale（注意这里是 FP32）

   weights = self.weights_proj(x.float()) * self.n_heads**-0.5
   weights = weights.unsqueeze(-1) * q_scale * self.softmax_scale
   

7. 核心 kernel fp8_index，可以看到这里是基于所有先前的 token 进行计算（注意是 :end_pos）

   index_score = fp8_index(
       q_fp8.contiguous(),
       weights,
       self.k_cache[:bsz, :end_pos].contiguous(),
       self.k_scale_cache[:bsz, :end_pos].contiguous(),
   )
   if mask is not None:
       index_score += mask
   

   略过封装，直接看 fp8_index_kernel：

   @tilelang.jit(out_idx=[4], pass_configs=pass_configs)
   def fp8_index_kernel(h: int, d: int):
       b = T.symbolic("b")
       m = T.symbolic("m")
       n = T.symbolic("n")
   
       blk_n1 = 512
       blk_n2 = 128
   
       @T.prim_func
       def fp8_index_kernel_(
           q: T.Tensor[(b, m, h, d), FP8],
           q_s: T.Tensor[(b, m, h), FP32],
           k: T.Tensor[(b, n, d), FP8],
           k_s: T.Tensor[(b, n), FP32],
           o: T.Tensor[(b, m, n), FP32],
       ) -> None:
           with T.Kernel(b, m, T.ceildiv(n, blk_n1)) as (i_b, i_m, i1_n):
               q_smem = T.alloc_shared((h, d), FP8)
               T.copy(q[i_b, i_m, 0, 0], q_smem)
   
               q_s_frag = T.alloc_fragment(h, FP32)
               T.copy(q_s[i_b, i_m, 0], q_s_frag)
   
               for i2_n in T.Pipelined(blk_n1 // blk_n2, num_stages=2):
                   k_smem = T.alloc_shared((blk_n2, d), FP8)
                   T.copy(k[i_b, i1_n * blk_n1 + i2_n * blk_n2, 0], k_smem)
   
                   k_s_frag = T.alloc_fragment(blk_n2, FP32)
                   T.copy(k_s[i_b, i1_n * blk_n1 + i2_n * blk_n2], k_s_frag)
   
                   logits = T.alloc_fragment((blk_n2, h), FP32)
                   T.gemm(
                       k_smem,
                       q_smem,
                       logits,
                       transpose_A=False,
                       transpose_B=True,
                       clear_accum=True,
                   )
   
                   for i_h, i3_n in T.Parallel(h, blk_n2):
                       logits[i3_n, i_h] = T.max(logits[i3_n, i_h], 0) * q_s_frag[i_h]
   
                   logits_sum = T.alloc_fragment(blk_n2, FP32)
                   T.reduce_sum(logits, logits_sum, dim=1)
   
                   for i3_n in T.Parallel(blk_n2):
                       logits_sum[i3_n] *= k_s_frag[i3_n]
   
                   T.copy(logits_sum, o[i_b, i_m, i1_n * blk_n1 + i2_n * blk_n2])
   
       return fp8_index_kernel_
   

   1. L18 为 Kernel 启动 ：grid.b 为 batch，grid.m 为 query token，grid.n 为 key token 的 chunk（512），即一个 query token 对应一个 kernel inst
   2. L19-20 将 query 加载到 shared memory 上，方便后续 key block 复用
   3. L25 对 key 进行 2-stage (load/compute overlap) 分块流水，每次处理 128 key tokens
   4. L32-40 计算 \(\text{logits}[n,h]=\sum_{d} k[n,d] \cdot q[h,d]\)，每个 key token 得到一个 \(h\) 维 tensor
   5. L43 有别于传统 Attention：
      • 用 ReLU 而不是 Softmax，不会放大负噪声、对 FP8 计算友好
      • 每个 head 有各自的 scale，避免 sparse 决策被某个 head 垄断；在 GEMM 后再 scale 避免精度损失
   6. L46 综合多个 head 计算 index score，在 L49 得到最后 dequant 的数值

8. 计算 topk_indices：所有 rank 参与计算、rank0 仲裁 index

   topk_indices = index_score.topk(min(self.index_topk, end_pos), dim=-1)[1]
   topk_indices_ = topk_indices.clone()
   dist.broadcast(topk_indices_, src=0)
   assert torch.all(
       topk_indices == topk_indices_
   ), f"{topk_indices=} {topk_indices_=}"
   return topk_indices
   

   单独在 rank0 上算了再 broadcast 会引入一次额外 AllReduce/Gather，而只同步 index 是最省带宽的

训练

使用 Linear 进行 mapping，需要进行训练，分别由 Dense Warm-up 和 Sparse Training 两个 stage 组成

Warm-up 用于初始化 Lightning Indexer，除 Lightning Indexer 外（实际就是除绿色通路外）的权重全部冻结：

• 为了使 index score 与最终 attn 分布对齐，将所有 attn head 的 score 加起来，经过 L1-正则化得到输出分布 \(p_{t,:}\in \mathbb{R}^t\)；定义 KL-散度损失作为 indexer 的训练目标函数 \(\mathcal{L}^I=\sum_{t} \mathbb{D}_\text{KL} \left(p_{t,:}\parallel \text{Softmax}(I_{t,:})\right)\) ，并取所有 token 来训练 indexer

• lr=1e-3，1000 steps，(16 seq * 128K tok) per step

Training 则是训练整个模型，其中模型和 indexer 的训练分开来：

• 对于 indexer，在原本的 \(\mathcal{L}^I\)上，仅关注被选中的 token set \(\mathcal{S}_t\)，不再是所有的 token；主模型依然按原始 loss 来训练
• lr=7.3e-6，2048 KV tok per Q tok，15000 steps，(480 seq * 128K tok) per step

推理

在 SGLang 中，DSA 的核心在 layers/attention/nsa 下 ，对于 DeepSeek 的封装则沿用 models/deepseek_v2.py

DSA 的引入将全量 Attn 替换为 Indexer + 2K (sparse) Attn，仍需完整存储整个序列的全量 Latent，同时 index cache 进一步引入 > 20% 的显存开销；为了提升 batch size，需要减少 GPU 上 latent cache， 全部卸载到 CPU 的话 Decode 计算时访问 Latent cache 会受限于带宽，因此直接的想法是能否采用局部 offload

局部 Offload

局部 offload 的前提是 latent cache 的访问要有足够 locality 才有效，否则触发一次 cache miss 就得不偿失；从 DSA 的设计看，与滑动窗口强制替换不同，过往被选中的token由于语义相似性，大概率在下一步也会被选中，有很强的时序局部性

在 LongBench V2 上的实验发现 latent cache 的 intra-layer 相似性 \(r_t^l=\cfrac{|K_{t-1}^l\cap K_t^l|}{|K_t^l|}\) > 80%，其中 \(K_t^l\) 表示第 \(l\) 层在第 \(t\) 步的 top-k index set，验证了 DSA 的强时序局部性

这能进一步确定使用 LRU 来替代原本的 FIFO 是最优的；在 Decode 刚启动时 cache 没有被填满所以会出现高 cache miss，直观做法就就是利用 prefill 的结果预填充 cache：在 ESS 中，将 prefill 阶段最后 32 windows 对应的 selected latent cache IDs 放入 GPU 上的 smem，取出对应的 cache entry 放入 GPU 上的 sparse memory pool 中

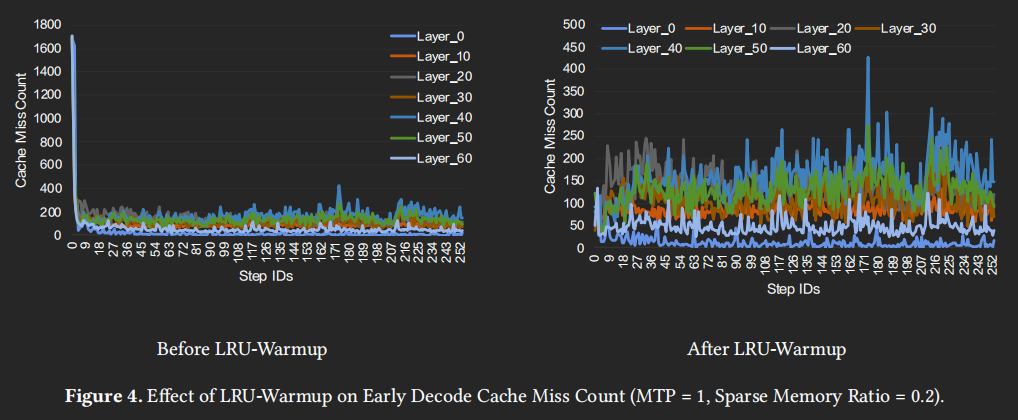
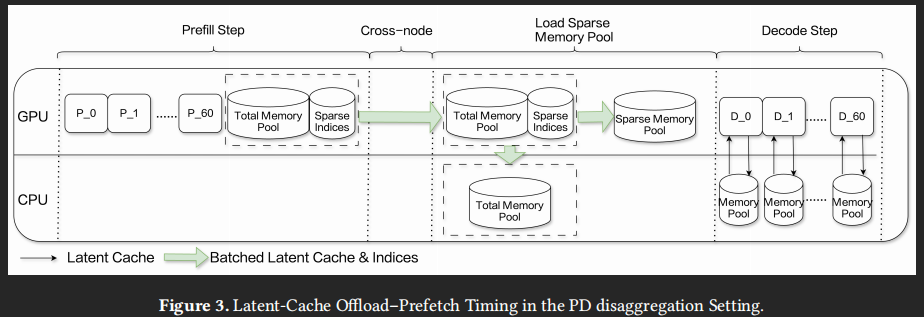
UVA 访存

在 SGLang 中 MLA 采用 PagedAttention 的 non-contiguous 存储、latent cache 单块仅 656 bytes（小块数据特征显著），导致频繁的小数据搬运，无法发挥 PCIe 的带宽（实测为 0.79 GB/s for H2D, 0.23 GB/s for D2H）

对此，可以基于 CUDA 的 UVA，设计 address-based on-demand transfer，来减少频繁 cudaMemcpyAsync 调用的开销（优化后达 37 GB/s for H2D, 43 GB/s for D2H）

• UVA + pinned host memory 后：CPU 内存和 GPU 显存共享 VA，GPU可以直接 L/S 访问 CPU内存，从 GPU page fault/cache miss 变成 GPU 主动发起 PCIe 读写
• GPU 可以自动 coalescing，IOMMU/ATS 将多个 page request 合成更大的 PCIe 传输，同时挂起大量未完成的 流式 PCIe request

DA + DBA Overlap

传输开销是不可避免的：Attn 启动前会触发 H2D 获取 missed latent cache，而 D2H 则将当前步新生成的 latent cache entry 写回 CPU；只能想办法 overlap，但在 SGLang 的原始实现中并没有做的很好：

class DeepseekV2AttentionMLA(nn.Module):
    def forward_absorb_prepare(
        self,
        positions: torch.Tensor,
        hidden_states: torch.Tensor,
        forward_batch: ForwardBatch,
        zero_allocator: BumpAllocator,
        llama_4_scaling: Optional[torch.Tensor] = None,
    ):
        from sglang.srt.model_executor.cuda_graph_runner import get_is_capture_mode

        q_lora = None
        if self.q_lora_rank is not None:
            q, latent_cache = (
                get_attn_tp_context()
                .fetch_qkv_latent()
                .split(
                    [self.q_lora_rank, self.kv_lora_rank + self.qk_rope_head_dim],
                    dim=-1,
                )
            )
            # k_nope = latent_cache[..., : self.kv_lora_rank]

            if self.alt_stream is not None and get_is_capture_mode():
                current_stream = torch.cuda.current_stream()
                self.alt_stream.wait_stream(current_stream)
                q = self.q_a_layernorm(q)
                # with torch.cuda.stream(self.alt_stream):
                # k_nope = self.kv_a_layernorm(k_nope)
                # current_stream.wait_stream(self.alt_stream)
            else:
                ...

            if self.use_nsa:
                q_lora = q

            # k_nope = k_nope.unsqueeze(1)
            # q = self.q_b_proj(q)[0].view(-1, self.num_local_heads, self.qk_head_dim)
        else:
            ...

        # q_nope, q_pe = q.split([self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1)
        # k_pe = latent_cache[..., self.kv_lora_rank :].unsqueeze(1)

        # if self.use_deep_gemm_bmm:
        #     q_nope_val, q_nope_scale, masked_m, expected_m, aligned_m = (
        #         per_token_group_quant_mla_deep_gemm_masked_fp8(q_nope.transpose(0, 1))
        #     )
        #     q_nope_out = q_nope.new_empty((self.num_local_heads, aligned_m, self.kv_lora_rank))
        #     deep_gemm_wrapper.grouped_gemm_nt_f8f8bf16_masked(
        #         (q_nope_val, q_nope_scale),
        #         (self.w_kc, self.w_scale_k),
        #         q_nope_out,
        #         masked_m,
        #         expected_m,
        #     )
        #     q_nope_out = q_nope_out[:, :expected_m, :]
        # else: ...

        # q_nope_out = q_nope_out.transpose(0, 1)

        if enable_prefill_cp(forward_batch, self.nsa_enable_prefill_cp):
            positions = cp_split_and_rebuild_position(forward_batch, positions)

        # if (
        #     self.rotary_emb is not None
        #     and (not self._fuse_rope_for_trtllm_mla(forward_batch))
        #     and (not _use_aiter or not _is_gfx95_supported or self.use_nsa)
        # ):
        #     q_pe, k_pe = self.rotary_emb(positions, q_pe, k_pe)

        # if enable_prefill_cp(forward_batch, self.nsa_enable_prefill_cp):
        #     k_nope, k_pe = self.rebuild_cp_kv_cache(latent_cache, forward_batch, k_nope, k_pe)

        topk_indices = None
        if q_lora is not None:
            topk_indices = self.indexer(
                x=hidden_states,
                q_lora=q_lora,
                positions=positions,
                forward_batch=forward_batch,
                layer_id=self.layer_id,
            )

        return ...

• self.indexer 的输入依赖只有 hidden_states + q_lora + positions

  • hidden_states 不变
  • L12-35：对 latent Q 作 layernorm 后赋值给 q_lora
  • L62-63：为了适应 context parallelism， positions 的编码方式可能会被重构

• 其余无关 self.indexer 的计算包括：

  • L22, 28-30：latent K 作 layernorm
  • L38：将 Q 投影到 attention head
  • L42-60：为后面的 MLA 提前计算好 Q No-RoPE 的部分，也就是 PreAttn
  • L65-73：PreAttn 的后处理

对此，ESS 将与 Indexer 无关的 PreAttn 计算后移，来掩盖一部分数据搬运，然后依次对 Attn 和 Indexer 切分来填补气泡

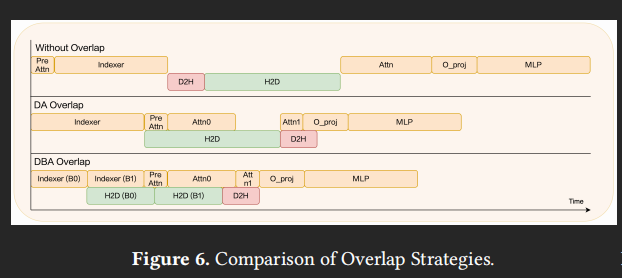
对于 Attn 可以进一步分成 "直接复用本地 latent cache 热数据" 和 "等待 H2D 换入冷数据" 这两个 kernel，前者执行计算时同步发起后者的数据请求，因此被称为 Dual Attn (DA) Overlap

更进一步，沿着 batch dim 切分 Indexer，先计算前半的 Indexer 后立即触发 H2D，让紧接着的后半 Indexer 和 PreAttn 来掩盖掉，此时前半能直接参与 Attn0 计算，实现气泡完全消除，也就是 DualBatch-Attn (DBA) Overlap

---

尽管如此，不同层内的 cache miss 行为存在显著差异，尤其是低 Sparse Memory Ratio（Sparse Memory Pool 相对 Total 的比例）的时候，意味着不能选用单一的 Overlap

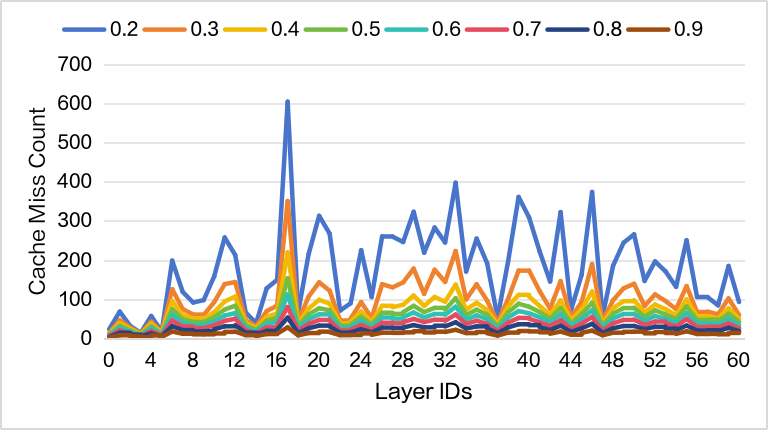
对此要先确定 在不同 context length 下各层的 cache miss 行为是否一致，从而确定每个层适合的 Overlap 策略:

• Sparse Memory Ratio=0.2（较小）时 cache miss 对比，当 context length = 32K 时，较小的 sparse memory 会触发频繁换入换出；对于较大的 context length，DSA 的设计使得 attn 始终集中在少数高频 token 上，每次 query 是机会命中的 KV block 数几乎恒定，更能实现反复 cache hit

  

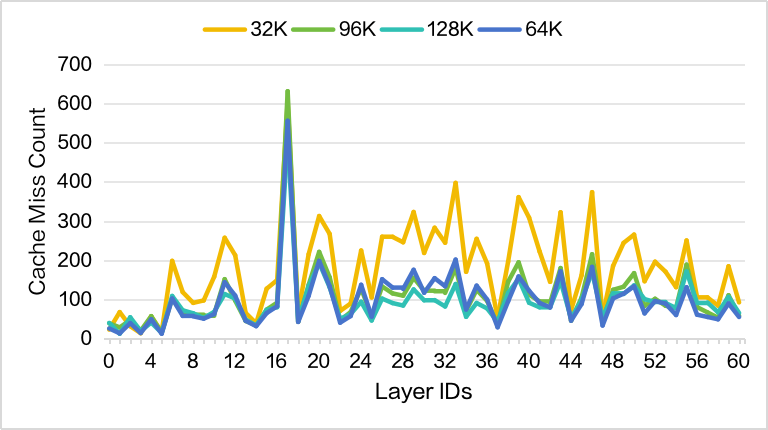
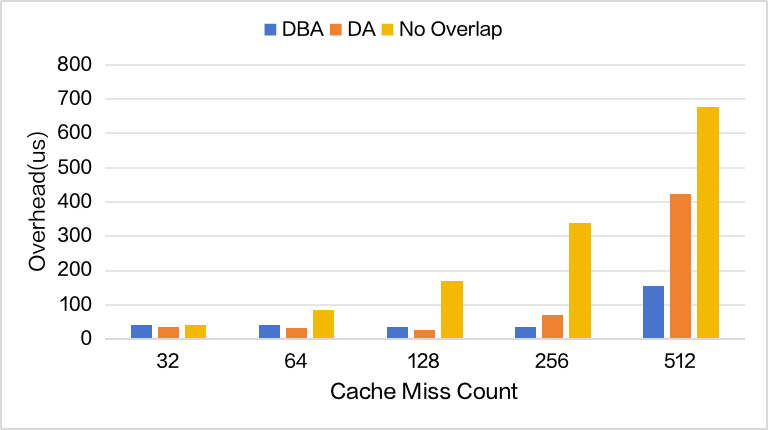
• 进一步对不同 cache miss count 分析三种策略的开销，由于 Indexer 的计算量随 context length 线性增加，DBA Overlap 能很好掩盖掉 latent cache 延迟；反之，DA Overlap 不引入 Indexer 划分，在短 context length 表现更好